Sin 2x = 2 sinx cosx Cos2x = 2 cos^2 x 1 So, (sin 2x)/(1cos 2x) = 2 sin x cos x /(1 2 cos^2 x 1) = 2 sin x cos x /2 cos^2 x = sin x /cos x = tan x For the second part,we have tanx = sin 2x/(1cos2x) Put x = 675° tan 675° = sin 135°/ 1 coCosine 2X or Cos 2X is also, one such trigonometrical formula, also known as double angle formula, as it has a double angle in it Because of this, it is being driven by the expressions for trigonometric functions of the sum and difference of two numbers (angles) and related expressions Let us start with the cos two thetas or cos 2X or cosine prove that cot x tan 2x1 =sec 2x lia cotx tan2x 1 = cotx * 2tanx/(1tan^2x) 1 = 2/(1 tan^2x) 1 = (2 (1 tan^2x))/(1 tan^2x) = (1 tan^2x)/(1 tan^2x) multiply top and bottom by cos^2x and you have = (cos^2x sin^2x)/(cos^2x sin^2x) = 1/cos2x = sec2x oobleck

Prove That Cos2x 1 Tan 2x 1 Tan 2x Youtube
Prove that cos2x=1-tan^2x/1+tan^2x
Prove that cos2x=1-tan^2x/1+tan^2x-Question 1tanx/1tanx = 1sin2x/cos2x prove Answer by htmentor(1303) (Show Source) You can put this solution on YOUR website! Prove that 1cos2x÷1cos2x=tan^2x 1 See answer soumojeetc2 is waiting for your help Add your answer and earn points Mahijaan Mahijaan Answer 1cos2x=2sin^2x 1cos2x=2cos^2x 2sin^2x/2cos^2x=tan^2x Hence proved New questions in
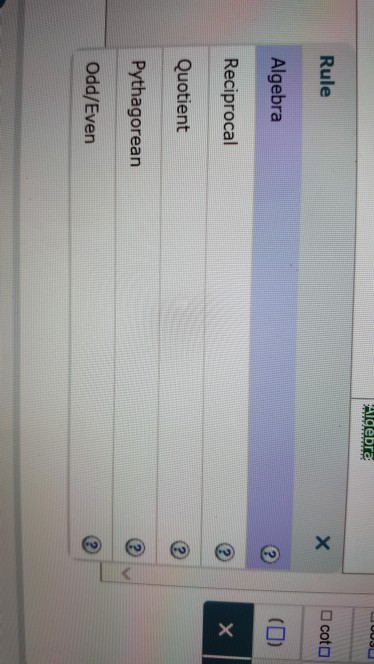



Prove The Identity Cos 2x 1 Tan 2x 1 Note That Chegg Com
How do you verify the equation is an identity?The limit of multiplication of the functions can be split as product of their limits as per the product rule of limits = ( lim x → 0 2 1 − tan 2 x) × ( lim x → 0 x tan 3 x ( 1 − cos 2 x) 2) Now, find the limit of the first factor by the direct substitution but do not disturb the second factorHINT We have that \frac{1\cos x}{\tan^2x}=\frac{\cos^2x(1\cos x)}{\sin^2x}=\frac{\cos^2x(1\cos x)}{1\cos^2x}=\frac{\cos^2x}{1\cos x} which is not an indeterminate form HINT We have that t a n 2 x 1 c o s x = s i n 2 x c o s 2 x ( 1 c o s x ) = 1 − c o s 2 x c o s 2 x ( 1 c o s x ) = 1 − c o s x c o s 2 x which is not an indeterminate form
(1cosx)/(1cosx) * (1cosx)/(1cosx) = (1cosx)^2 / (1 cos^2x) = (1cosx)^2/sin^2x = ((1cosx)/sinx)^2 = tan^2 x/2 from your halfangle formulasLearn how to solve trigonometric identities problems step by step online Prove the trigonometric identity 1/(tan(x)(1cos(2x)))=csc(2x) Apply the trigonometric identity \cos\left(2x\right)1=2\cos\left(x\right)^2 Since \cos is the reciprocal of \sec, \frac{1}{2\tan\left(x\right)\cos\left(x\right)^2} is equivalent to \frac{\sec\left(x\right)^2}{2\tanTo prove 1 tan² x /1 tan² x = cos 2x => let, LHS = 1 tan² x / 1 tan² x now, tan x = sin x / cos x so, LHS = 1 (sin² x / cos² x) / 1 (sin² x / cos² x) LHS = (cos² x sin² x) / cos² x / (cos² x sin² x) / cos² x LHS = (cos² x
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!To Prove that tan − 1 (1 3 ⋅ tan x) = 1 2 ⋅ cos − 1 (1 2 cos 2 x 2 cos 2 x) Let tan x = 3 ⋅ tan θ (E01) θ = tan − 1 ( tan x 3 )Q Solve the following trig equations 2 sec2 x tan2 x − 3 = 0 sec x tan x = 1 2 cos2 x2 −√2 = 0 A Consider the equation 2sec2xtan2x3=013sec2x2sec2x=043sec2x=0secx=233, secx=233x=π62πn, x=




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




Find Sin 2x Cos 2x And Tan 2x If Tan X 12 5 And X Terminates In Quadrant I Study Com
Prove that `(1 sin 2x cos 2x)/(1 sin 2x cos 2x) =tan x`Proof Half Angle Formula tan (x/2) Product to Sum Formula 1 Product to Sum Formula 2 Sum to Product Formula 1 Sum to Product Formula 2 Write sin (2x)cos3x as a Sum Write cos4xcos6x as a Product Prove cos^4 (x)sin^4 (x)=cos2x Prove sinxsin (5x)/ cosxcos (5x)=tan3xProve \cot(2x)=\frac{1\tan^2(x)}{2\tan(x)} en Related Symbolab blog posts High School Math Solutions – Trigonometry Calculator, Trig Identities In a previous post, we talked about trig simplification Trig identities are very similar to this concept An identity



How To Prove That 1 Sin 2x 1 Cotx Cos 2x 1 Tanx Sinxcosx Using Trig Identities Quora
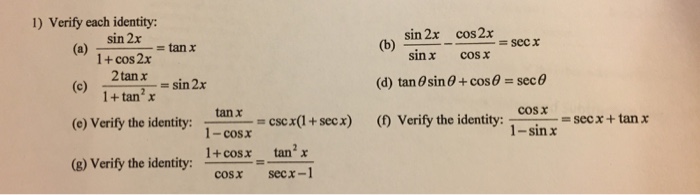



Verify Each Identity A Sin 2x 1 Cos 2x Tan X Chegg Com
Get an answer for 'Prove that `(1cos^2x)(1cot^2x)=1`' and find homework help for other Math questions at eNotesProve that (1tanx)/(1tanx) = (1sin2x)/cos2x Replace tanx with sinx/cosx For the denominator, cos^2x sin^2x = cos2x So (1tanx)/(1tanx) = (1sin2x)/cos2x Ex 33, 23 Prove that tan4𝑥 = (4 tan〖𝑥 (1−tan2𝑥)〗)/(1 − 6 tan2 𝑥tan4 𝑥) Taking LHS tan 4x We know that tan 2x = (2 𝑡𝑎𝑛𝑥)/(1 − 𝑡𝑎𝑛2 𝑥) Replacing x with 2x tan (2 × 2x) = (2 𝑡𝑎𝑛2𝑥)/(1 − 𝑡𝑎𝑛2 2𝑥) tan 4x = (2 𝑡𝑎𝑛2𝑥)/(1 − 𝑡𝑎𝑛2 2𝑥) = (2 ta



How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora




Ppt Analytic Trig Powerpoint Presentation Free Download Id
Click here 👆 to get an answer to your question ️ prove that 1sin2x/1sin2x=tan^2(pi/4x)Answer to Prove the identity 1 cos(2x)/sin(2x) = tan(x) 1Prove sin^2 (x)= 1/21/2 cos (2x) \square!




Let Tan 2x 1 2tan 2 Y Then Prove That Cos 2y 1 2cos 2x



3
2cos^2xsinx=1 solution Education Details Solution for 2cos^2xsinx=1 equation Simplifying 2cos 2 x 1sinx = 1 Solving 2cos 2 x 1insx = 1 Solving for variable 'c' Move all terms containing c to the left, all other terms to the right Add 'insx' to each side of the equation 2cos 2 x 1insx insx = 1 insx Combine like terms 1insx insx = 0 2cos 2 x 0 = 1 insx 2cos 2 x = 1 Get an answer for 'Show that `tan^2 x = (1 cos(2x))/(1 cos(2x))`' and find homework help for other Math questions at eNotes Prove that `sec^4(x)tan^4(x)=1tan^2(x)` 3 Educator answersTanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx Integral of the function \frac {\cos ^2 x} {1\tan x}




Sin2x Cos2x 1 Proof




Cos 2x 1 Tanx Sin 3x Sinx Cosx 1 Sinx Cosx Brainly In
Prove each identity a) 1cos^2x=tan^2xcos^2x b) cos^2x 2sin^2x1 = sin^2x I also tried a question on my own tan^2x = (1 – cos^2x)/cos^2x RS= sin^2x/cos^2x I know that the Pythagorean for that is sin^2x cos^2x That's all I could doLHS= Sin 2x /( 1 cos2x ) We have , sin 2x = 2 sinx•cosx And cos2x = 2cos^2 x 1 ie 1 cosx 2x = 2cos^2x Putting the above results in the LHSwe get, Sin2x/ ( 1 cos2x ) =2 sinx•cosx/2cos^2x =sinx / cosx = Tanx • sin2x/(1 cos2x)= tanxTan^2xtan^2y=sec^2xsec^2y and, how do you factor and simplify, cscx(sin^2xcos^2xtanx)/sinxcosx mathtrig Use the double angle identities to find sin2x if sinx= 1/square of 17 and cosx Math How many solutions does the equation cosx 1/2 = 1 have for 0
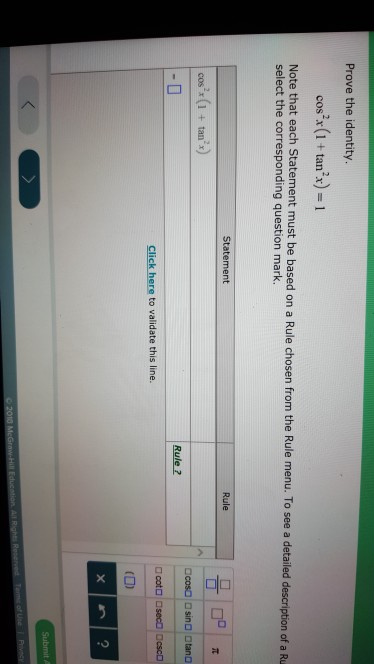



Prove The Identity Cos 2x 1 Tan 2x 1 Note That Chegg Com




Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55
Use the ff doubleangle trigonometric identities sin2A=2sinAcosA cos2A=12sin^2(A) cos2A=2cos^2(A)1 cotA=cosA/sinA now lets start by substituting identities since we want to factor the numerator by cosA and denominator by sinA Get an answer for 'Prove that `sec^4(x)tan^4(x)=1tan^2(x)` ' and find homework help for other Math questions at eNotes prove that 1cos2x÷1cos2x=tan^2x 'Show that `tan^2 x = (1 cos(2x))/(1 cos(2x))`'tan^2x=1cos2x/1cos2x true or false1cos2x/1cos2x is equal to1cos2x/1




The Pythagorean Trigonometric Identity Sin 2 X Cos 2 X 1



Q Tbn And9gcr2jamezvnschsup9wyxdzj0wc0knie4dqfphj6okqiboct8vn1 Usqp Cau
Express sec2x in terms of tanx and secx I know you have to sec(2x) = 1/cos(2x) = 1/(cos²x sin²x) But how do you split that Like how to simplify that?Get an answer for 'trigonometry Prove that cos2x(1 tanx*tan2x) = 1' and find homework help for other trigonometry math questions at eNotes Search this site Go (1 tan x*tan 2x) = 1Set matht=x/2/math and recall that math\cos2t=2\cos^2t1/math so you have math\frac{2}{1\cos x}\tan^2\frac{x}{2}=\frac{2}{2\cos^2t}\frac{\sin^2t}{\cos^2t




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic



Prove The Identity Cos 2x 1 Sin 2x Tan P 4 X Sarthaks Econnect Largest Online Education Community
We have to prove $$\frac{1}{\tan(x)(1\cos(2x))}=\csc(2x)=\frac{1}{\sin(2x)}$$ Multiply both sides by $\tan(x)$ and apply $\sin(2x)=2\sin(x)\cos(x)$ and you arrive at $$\frac{1}{2{\cos^2(x)}}=\frac{1}{1\cos(2x)}$$ raise both sides to the power of 1, and divide both sides by two and arrive at $$\cos^2(x)=\frac{1}{2}\frac{1}{2}\cos(2x)$$ which is a wellknownQuestion Decide whether the equation is a trigonometric identiye explain your reasoning cos^2x(1tan^2x)=1 secxtanx(1sin^2x)=sinx cos^2(2x)sin^2=0Given,cos2x cos4x = 1cos4x = 1 cos2xcos4x = sin2xcos2x cos2x= sin2x Given,cos2x cos4x = 1cos4x = 1 cos2xcos4x = sin2xcos2x cos2x= sin2x Previous Year Papers Download Solved Question Papers Free for Offline Practice and view Solutions Online If cos 2 x cos 4 x = 1, then tan 2 x tan 4 x = ?



Www Alamo Edu Contentassets 35e1aad11a064ee2ae161ba2ae3b2559 Analytic Math2412 Double Angle Power Reducing Half Angle Identities Pdf
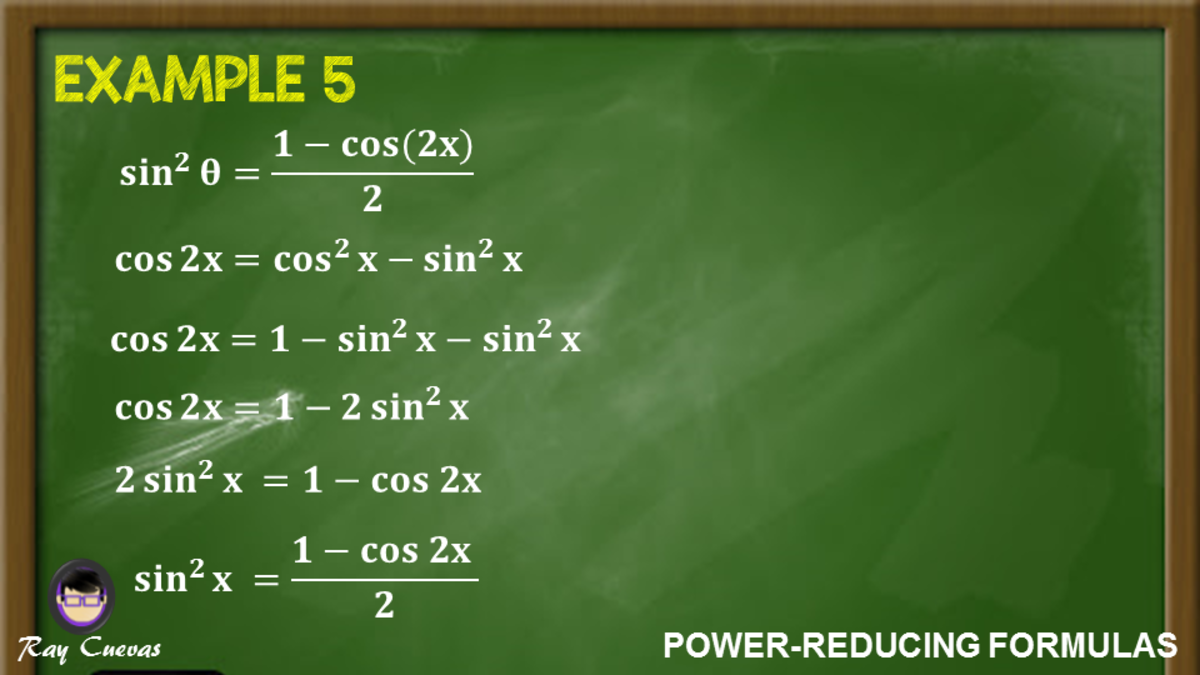



Power Reducing Formulas And How To Use Them With Examples Owlcation
I am unable to see why $$1 \tan^2 x= 1/\cos^2x$$ I have looked into the topic anad I am familiar with the reciprocal ratios of cosec, sec, and cot but cannot derive how this statement makes sense Any help on the topic would be very much appreciatedGet an answer for 'Prove that `1 2*cos^2x = (tan^2x 1)/(tan^2x 1)`' and find homework help for other Math questions at eNotes(1tan^2x)/(1tan^2(x)) 1 = 2cos^2(x)
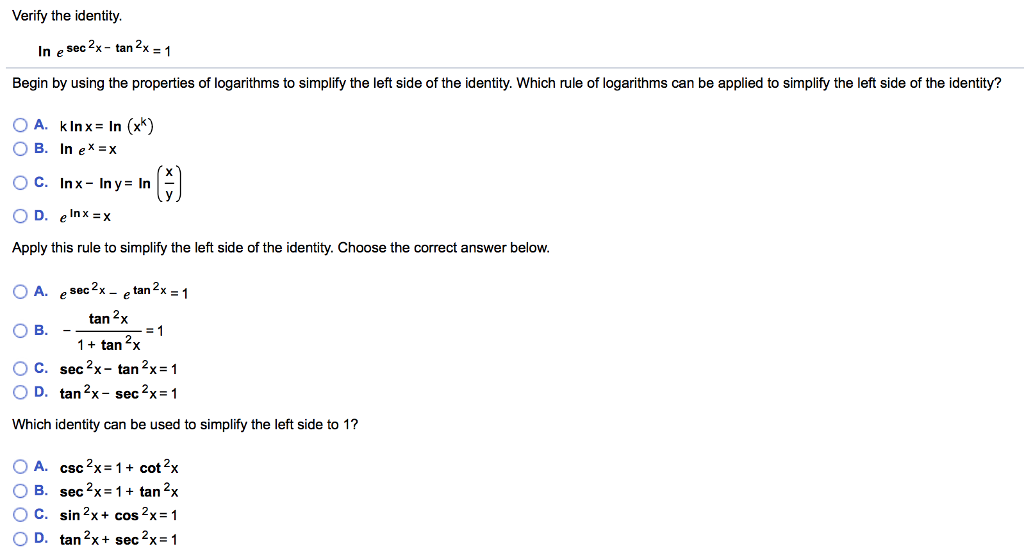



Verify The Identity In Esec 2x Tan 2x 1 Begin By Chegg Com




Tangent Half Angle Formula Wikipedia
0 1 2tan 2 x 2tan 4 x B 1 cos 2x/(1 sin 2x) As we know that, cos 2x = cos 2 x – sin 2 x Sin 2x = 2 sin x cos x Therefore, On multiplying numerator and denominator by 1/√2 = RHS Thus proved If 4^(sin2x 2cos^2x) 4^(1 sin2x 2sin^2x) = 65, then (sin2x cos2x) has the value equal to asked in Mathematics by Taniska ( 645k points) jee



bestpictjcry Tan 2x Tan 2x




Inverse Trigonometric Functions General Solution Of
Cosx cos2x = 1 cos x = 1 cos2x cos x = sin2x (i)Again, cosx cos2x = 1Cubing both sides, we get(cos x cos2x)3 = (1)3cos3x (cos2x)3 3 cosx x cos2x cos x cos2 x = 1cos3x cos6x 3 cos3xcos x cos2x = 1cos3x cos6x 3 cos4x 3cos5x 1 = 0Now, put cosx = sin2x From equ (i)(sin2x)3 (sin2x)6 3(sin2x)4 3(sin2x)5 1 = 0 sin12x 3 sin10x 3 sin8x sin6x 1Math angle x lies in the third quadrant and tanx=7/24 determiner an exact value for cos2x determiner an exact value for sin2x Math please help quickSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




2 14pts Prove The Given Identities A Tan 2 1 Tan 1 Cos B Cos 1 Sino Homeworklib




Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction
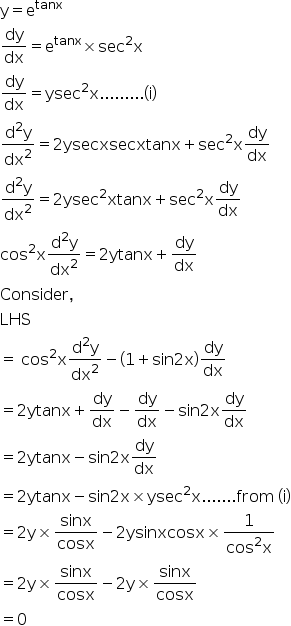



If Y Etan X Prove That Cos2 X D2y Dx2 1 Sin 2x Dy Dx 0 Explain In Great Detail Mathematics Topperlearning Com Mbti5k33



2
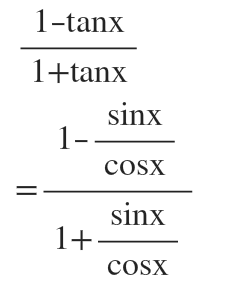



Answered Prove The Following Identity 1 Tan X Bartleby



Q Tbn And9gcqyhylzm7bpns9hs 3u 9a8zjac1zopdmmfnvrmoregmsc5as7c Usqp Cau




Answered Prove The Following Identity 1 Tan X Bartleby




For 1 Through 4 Prove The Following Identities 1 Chegg Com




Mapping Your Mind By Kyanna Dyer




Sin2x Cos2x 1 Proof
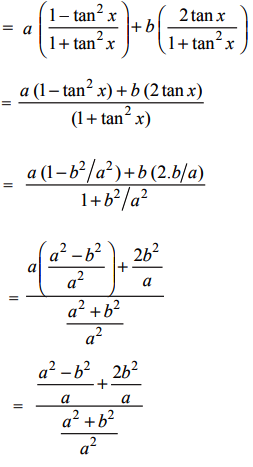



If Tan X B A Then The Value Of A Cos 2x B Sin 2x Is



Why Does The Example Not Include Cos2x 0 The Student Room



Solved Explian The Proof For This Tan 2x 1 Tan X Co5 2x Solution Starting With The Left Side Sin 2x Sm X Step 1 Cos 2x Cos X Sin 2x Course Hero




Prove The Identity 1 Tan 2x 1 Tan 2x 1 2sin 2x In Urdu Hindi Youtube




Prove That 1 Cos 2x Cos 2x Tan 2x Wyzant Ask An Expert




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




If Tan X 2tan 2y 1 Then Show Cos2x Sin 2y 0 Z X And Deduce That Tan 750 T Tan X Tan 4 X Maths Trigonometric Functions Meritnation Com




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube




Prove That Cos2x 1 Tan 2x 1 Tan 2x Youtube



Sites Math Washington Edu Putnam Handouttrig Pdf




Tan2x ただの悪魔の画像




Ex 7 2 25 Integrate 1 Cos 2 X 1 Tan X 2 Ex 7 2




Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf




How Do You Prove Tan 2x Secx 1 1 Secx Socratic



A 1 Tan X Tan X 1 Show That A Ta 1 Cos 2x Sin 2x Sin 2x Cos 2x Sarthaks Econnect Largest Online Education Community




Tan2x ただの悪魔の画像




Tan 2 X Tan 2 X 1 Cosec 2 X Sec 2 X Cosec 2 X 1 Sin 2 X Cos 2 X Brainly In



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero




How To Prove The Identity Sin 2x Cos 2x 1 Enotes Com




8 Prove That Cos2x 1 Tan 2x 1 Tan 2x Brainly In




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download




Cos2x 1 Tan Square X 1 Tan Squre X Brainly In
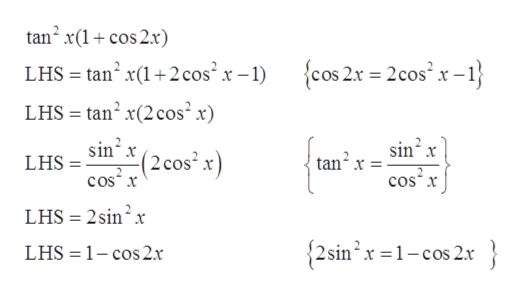



Answered Tan2x 1 Cos2x 1 Cos2x Verify The Bartleby
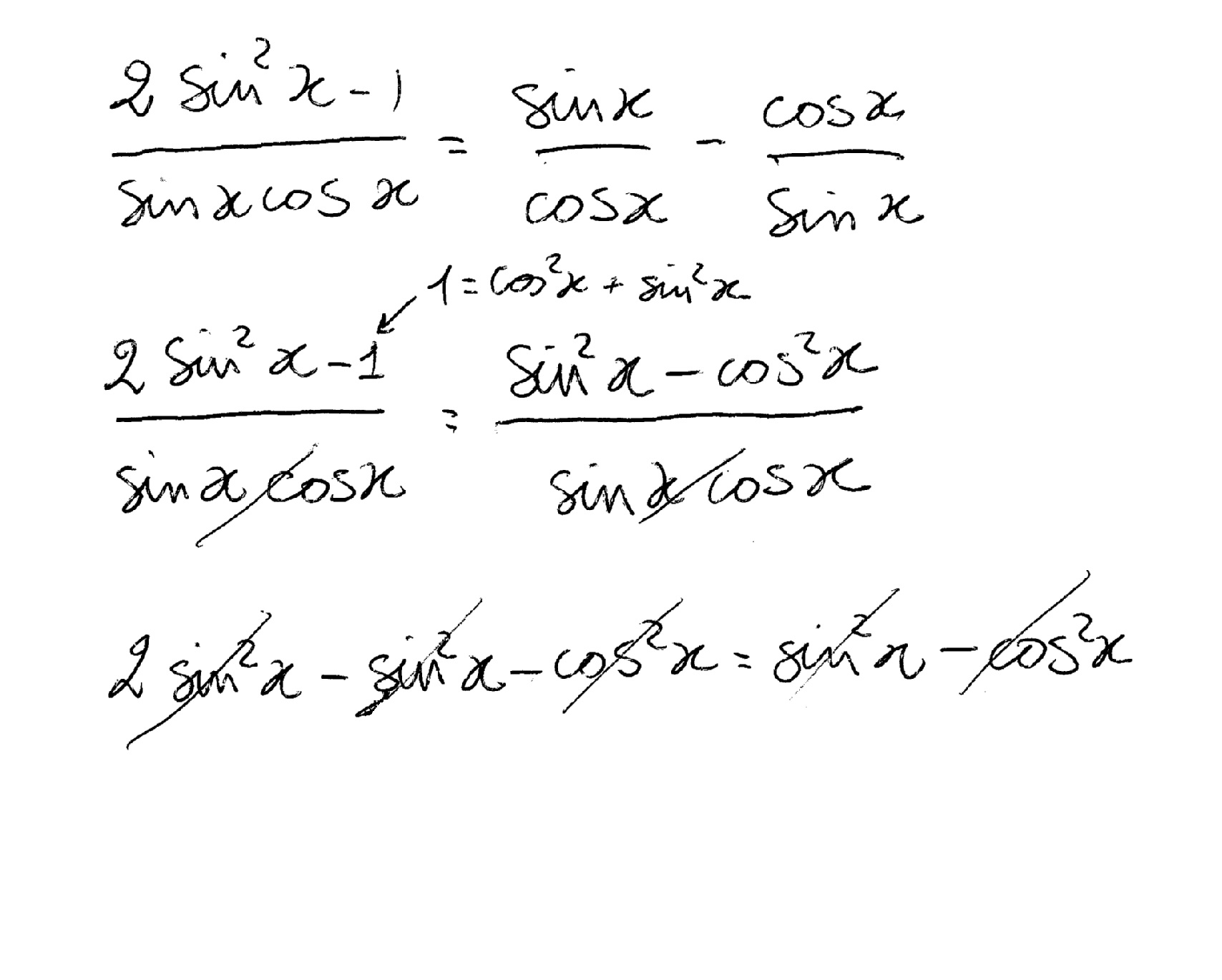



How Do You Prove 2sin 2x 1 Sinxcosx Tanx Cotx Socratic




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube
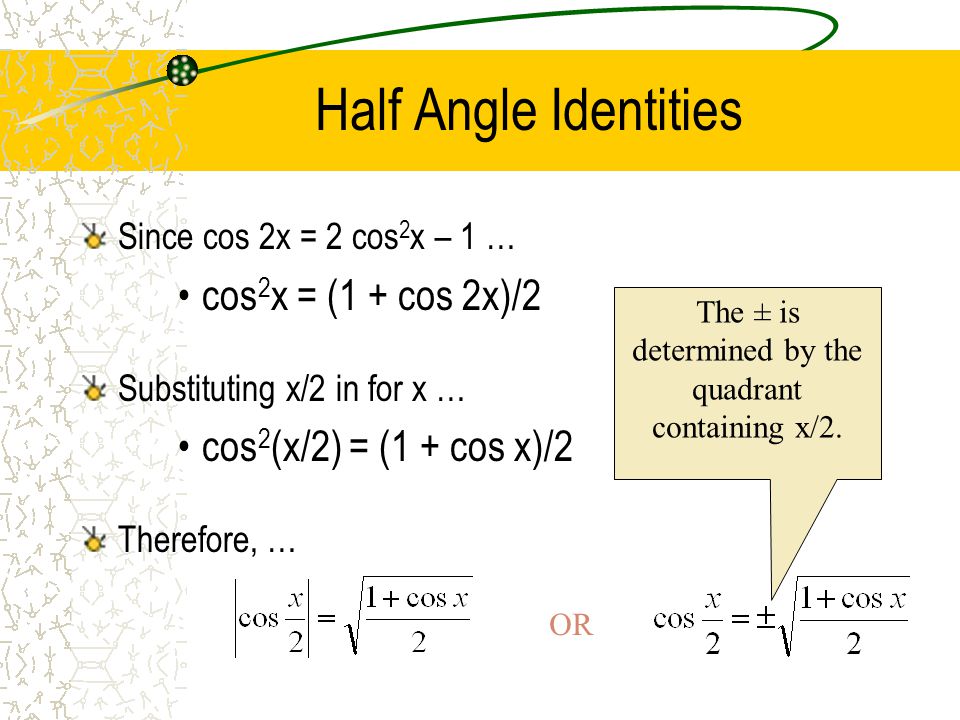



Section 2 Identities Cofunction Double Angle Half Angle Ppt Video Online Download




Double Angle Formulas What Are Double Angle Formulas Examples




Analytic Trig Trig Identities Sin 2x Cos 2x 1 Tan 2x 1 Sec 2x 1 Cot 2x Csc 2x Sin X Sinx Cos X Cosx Tan X Tanx Ppt Powerpoint



Opjsrgh In Content Worksheet Practice Ws Day169 11 Maths Pdf




Prove That 1 Sin2x Cos2x Sin2x Cos2x Tanx Maths Meritnation Com




1 Cos 4 X Sinº X Cos 2x 6 6 2 Sin X Cos X Homeworklib



7 Proving Ids Trig Functions Identities




Lecture 126 Proof Cos 2 X 1 Cos2x 2 Cosmolearning Mathematics




Solve Tan 2 X 1 0 Yahoo Answers Noha Matthieu Lire Un Livre



How Do We Prove That Tan2x 1 Sec2x Tanx Quora




If F 2tanx 1 Tan 2x Cos2x 1 Sec 2x Tanx 2 Then F X




Ch 7 Trigonometric Identities And Equations Ppt Video Online Download



Classroomweb Pusd11 Net Sites Mmalmos Shared documents Precalculus honors Chapter 5 analytic trigonometry Hw ch 5 Pdf




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




B Prove Each Of The Following Identities I Sin 2 Gauthmath



2



Can You Prove A Trig Identity Making The Right Side Equal To The Left Side For Example 1 Sin2x Cos2x 1 Tanx 1 Tanx If No To The Question Why Quora




If Tan 2 X Cos 2 Y Sin 2 Y Then Prove That Cos 2 X Cos 2 X Tan 2 Y



Splash Tdchristian Ca Classes Math Textbooks Mhf4uetext Afsb 412 Pdf




Prove Tan2x 2tanx 1 Tan 2 X Maths Introduction To Trigonometry Meritnation Com




Tan X 2 1 Cos 2x 1 Cos 2x Youtube



Www Birmingham K12 Mi Us Cms Lib Mi Centricity Domain 976 Chapter 5 Pdf
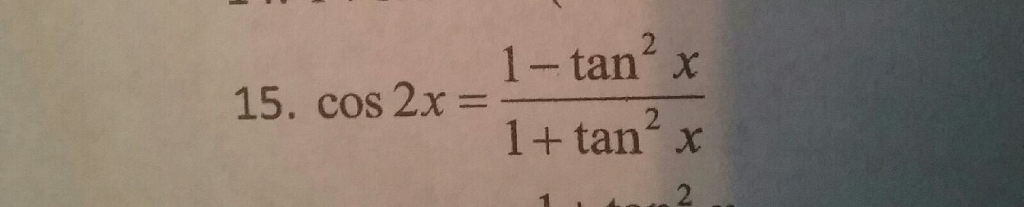



Prove The Identity Cos 2x 1 Tan 2 X 1 Tan 2 X Chegg Com



Ilectureonline




Prove Int 0 Pi 2 Frac 1 2 Cos 2x Cdot Ln Tan X 1 Tan 2 Sqrt 2 X Tan 1 Sqrt 2 X Dx 0 Newbedev
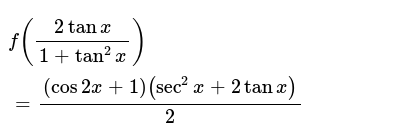



F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2
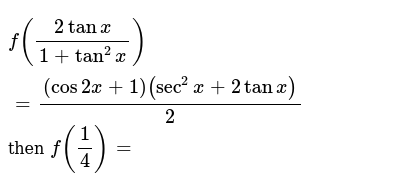



F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2 Then F 1




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Prove That Tan3xtanx 2cos2x 12cos2x 1




Solve Int1 Cos 2x 1 Tanx 2dx



Prove That Cos2x Cos 2x Sin 2x 2cos 2x 1 1 2sin 2x 1 Tan 2x 1 Tan 2x Sarthaks Econnect Largest Online Education Community




Prove The Following Trigonometric Identities Show Gauthmath




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube



How To Prove Math Dfrac Sqrt 1 Cos 2x 1 Cos 2x Tan X Math Quora




Prove That 1 Sin 2x Cos 2x 1 Sin 2x Cos 2x Tan X




How To Prove The Identity Sin 2x Cos 2x 1 Enotes Com



Solved Explian The Proof For This Tan 2x 1 Tan X Co5 2x Solution Starting With The Left Side Sin 2x Sm X Step 1 Cos 2x Cos X Sin 2x Course Hero



Prove That Cos2x Cos 2x Sin 2x 2cos 2x 1 1 2sin 2x 1 Tan 2x 1 Tan 2x Sarthaks Econnect Largest Online Education Community



Q Tbn And9gctufmrsc12qufe Whtfdvvuwzj Z1m2v6 P T5bb9h Rcw17hdb Usqp Cau




Prove That I Sin 2x 1 Cos 2x Cot X Ii 1




Prove The Following Identities A Cot X Sec X C Gauthmath




Prove That The Equations Are Identities 1 Chegg Com




Prove The Identity Cos 2x 1 Tan 2x 1 Note That Chegg Com




Cos2x 1 Sin2x Tan Pi 4 X Double And Half Angle Identity Youtube




Sin2x Cos2x 1 Proof



How Do You Verify Cos 2x Sin 2x 1 Cos 2x Csc 2x Socratic




Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube



0 件のコメント:
コメントを投稿